Here we will discuss math behind backpropagation in neural network. Here are the prerequisites for this tutorial.

• Matrix, Vectors
• Dot product, Element-wise multiplication
• Matrix Calculus(Chain Rule)
• Gradient Descent Algorithm

Let us consider a 2 layered Artificial Neural Network as shown in the figure below. 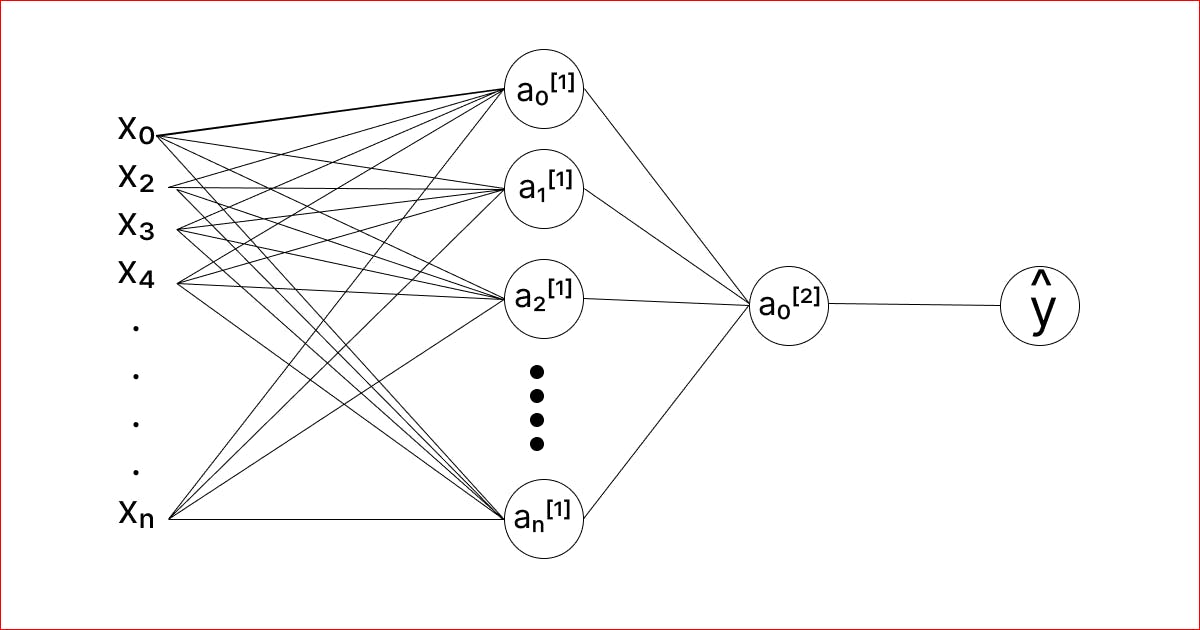There are two hidden layers(including the output layer). The output activation function is supposed to be a sigmoid function. And activation function is any other function (say g(x)).

Background

Neural Networks are first initialized with random parameters for every layers. Our objective is to correct these parameters to obtain the best fit. We use gradient descent algorithm which corrects the randomly initialized parameters at each iterations. For this, at each epochs forward propagation is performed which generates intermediate and final output using the current parameters. Then, cost for that result is calculated. Then, there comes a bad boy, backpropagation. Backpropagation uses cost to calculate gradients and then comes the gradient descent.

Forward Propagation

To start forward propagation, parameter matrix (W) needs to be initialized randomly for all layers. Then, forward propagation proceed as below. $$ Z^{[1]} = W^{[1]}X + b^{[1]}$$ $$A^{[1]} = g^{[1]}(Z^{[1]})$$ $$ Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$$ $$A^{[2]} = g^{[2]}(Z^{[2]}) = \sigma(Z^{[2]})$$ Note: \(\sigma \) denotes sigmoid function. ie \(\sigma =\frac{1}{1+e^{-z^{[2]}}} \)

Back Propagation

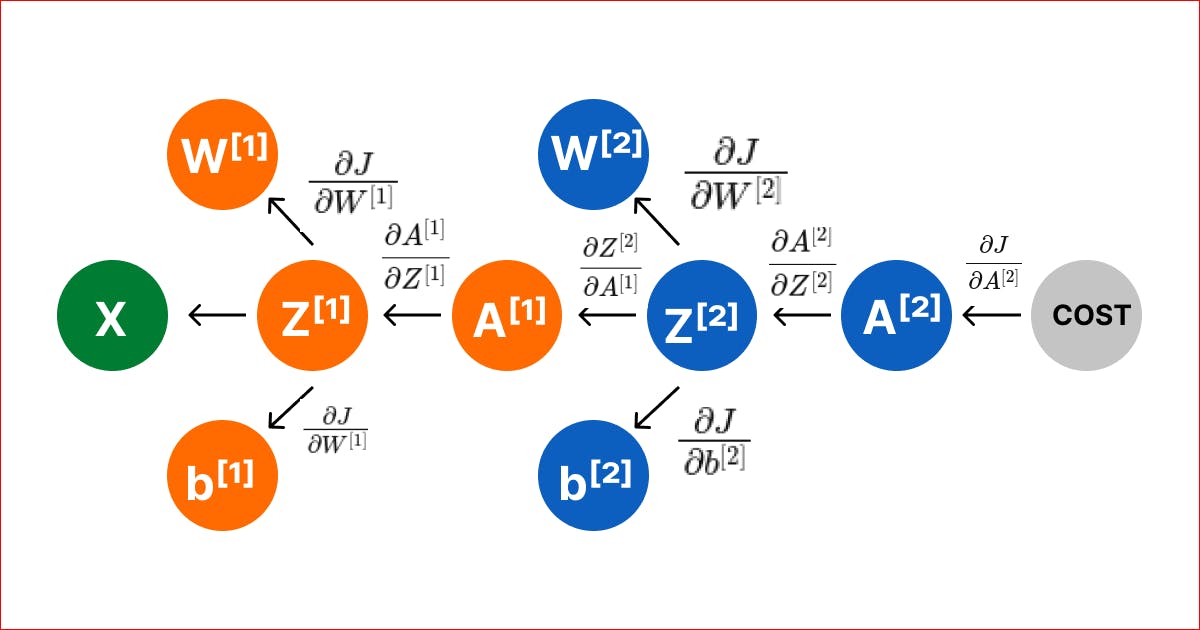$$fig: Computational\,Graph\, for\,Back\,Propagation$$ In our two layered Neural Network, we have four parameters \(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]}\) Note: Superscript [l] denotes parameters of \(l^{th}\) layer. So, to update these parameters using gradient descent we need to calculate the respective gradients \(\frac{\partial J}{\partial W^{[2]}}, \frac{\partial J}{\partial b^{[2]}}, \frac{\partial J}{\partial W^{[1]}}, \frac{\partial J}{\partial b^{[1]}}\)

Chain rule of derivative will come in handy while calculating these gradients. $$ \frac{\partial J}{\partial W^{[2]}} = \frac{\partial J}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \frac{\partial Z^{[2]}}{\partial W^{[2]}}$$ For further simplification, we will calculate each product terms on RHS one by one. $$ \frac{\partial J}{\partial A^{[2]}} = \sigma'(Z) = \frac{d(1+e^{-Z})^{-1}}{dZ} $$ $$= \frac{e^{-Z}}{(1+e^{-z})^{2}} = \frac{1}{1+e^{-Z}}*\frac{1+e^{-Z}-1}{1+e^{-Z}} $$ $$ = \sigma(Z)(1- \sigma(Z)) $$ Then, $$ \frac{\partial J}{\partial A^{[2]}} = \frac{\partial (-Ylog(A^{[2]}) - (1-Y)log(1-A^{[2]}))}{\partial A^{[2]}} $$ $$ = -\frac{Y}{A^{[2]}} - \frac{1-Y}{1-A^{[2]}} = \frac{A^{[2]}-Y}{A^{[2]}(1-A^{[2]})}$$

Similarly, $$\frac{\partial Z^{[2]}}{\partial W^{[2]}} = \frac{\partial (W^{[2]}A^{[1]} + b^{[2]})}{\partial W^{[2]}} = A^{[1]}$$ Hence, $$\frac{\partial J}{\partial W^{[2]}} = (A^{[2]}-Y).A^{[1]} $$ Great! Next we will calculate gradient of \( b^{[2]} \) in similar way. $$ \frac{\partial A}{\partial b^{[2]}} = \frac{\partial J}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \frac{\partial Z^{[2]}}{\partial b^{[2]}}$$

For this, first two terms are already calculated. $$ \frac{\partial Z^{[2]}}{\partial b^{[2]}} = \frac{\partial (W^{[2]}A^{[1]} + b^{[2]})}{\partial b^{[2]}} = 1$$ Hence, \(\frac{\partial Z^{[2]}}{\partial W^{[2]}} =A^{[2]}-Y\)

Next, we will calculate the gradients for first hidden layer \(\frac{\partial J}{\partial W^{[1]}}, \frac{\partial J}{\partial b^{[1]}}\).

$$ \frac{\partial J}{\partial W^{[1]}} = \frac{\partial J}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \frac{\partial Z^{[2]}}{\partial A^{[1]}} \frac{\partial A^{[1]}}{\partial Z^{[1]}} \frac{\partial Z^{[1]}}{\partial W^{[1]}}$$ First two terms are already calculated. $$ \frac{\partial Z^{[2]}}{\partial A^{[1]}} = W^{[2]} \hspace{0.3cm}and \hspace{0.3cm} \frac{\partial Z^{[1]}}{\partial W^{[1]}}= X$$

Hence, \( \frac{\partial J}{\partial W^{[1]}} = (A^{[2]}-Y).W^{[2]}* g^{[1]}{'}(Z^{[1]}).X \) Similarly, we can calculate gradient for bias term b for first layer.

\( \frac{\partial J}{\partial b^{[1]}} = (A^{[2]}-Y).W^{[2]}* g^{[1]}{'}(Z^{[1]}) \)

Finally we can compute updated weight using gradient descent as below.

$$ W^{[2]}-= \alpha * \frac{\partial J}{\partial W^{[2]}} $$

$$ b^{[2]}-= \alpha * \frac{\partial J}{\partial b^{[2]}} $$

$$ W^{[1]}-= \alpha * \frac{\partial J}{\partial W^{[1]}} $$

$$ b^{[1]}-= \alpha * \frac{\partial J}{\partial b^{[1]}} $$

Above explanation is only the intuition to understand math behind back propagation in Neural Network. Exact coding implementation differ slightly with use of numpy function like dot product and sums. Also, in real implementation there are multiple training examples, so these formulae needs to be adjusted accordingly.